文脈自由文法とは
文脈自由文法の定義
Hopcroftらによる定義[1]をもとに説明する.
文脈自由文法Gは4つの要素を用いて以下のように表される.
G = (V, T, P, S)
V: the set of variables
T: the terminals
P the set of productions
S: the start symbolそれぞれについて詳しく説明した後, 例を紹介する.
Tは終端文字. 記号からなる有限の集合.
Vは非終端文字. 変数からなる有限の集合. なお, 各変数は, 言語を表す.
言語は, 次のように定義される文字列の集合.
A set of strings all of which are chosen from some Σ*, where Σ is a particular alphabet, is called a language. - Hopcroft et.al. (1979). Introduction to Automata Theory, Languages, and Computation (1st ed). 1.5.3 LanguagesSは開始記号. 今回の文脈自由文法で定義する言語を表す変数.
Pは生成規則. 再帰的に言語を定義するためのいくつかのルールたち. 以下の要素で構成される
- その生成規則によって(部分的に)定義されるようになる変数.
- 生成を表す記号 “→”
- 変数または終端文字を0個以上並べた文字列.
文脈自由文法の例
文脈自由文法Gが以下のように定義されているとする.
G = ({P}, {0, 1}, A, P}
ただし, Aは以下の5つの生成規則からなる集合
P -> ε
P -> 0
P -> 1
P -> 0P0
P -> 1P1この文脈自由文法によって表される言語Lは以下の通り.
L = {w | w = wr}
※ wrはwを逆から読んだもの. アルファベットが{0, 1}の時の回文を表す.
チョムスキー階層による文法の分類
文脈自由文法はチョムスキー階層では, Type-2に分類される[2].
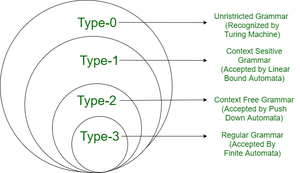
Type-1は, 文脈依存言語(Context-sensitive Language)と呼ばれる言語. Hopcroftでの説明[1]をいかに引用する
There is a more powerful classes of grammars, called "context-sensitive," where replacements are permitted only if certain strings appear to the left and/or right. Context-sensitive grammars do not play a major role in practice today.要は, 生成規則の矢印の左側に変数または終端文字が2つ以上並ぶ規則だったら, 文脈依存言語になる.
例えば, anbncn は以下の生成規則で表される文脈依存言語[3].

Type-3は, 正規言語. オートマトンによって受理されることを抑えておきたい. ここでは詳細な説明は省く.
構文解析器
文脈自由文法で表される言語を構文解析器(パーサー)によって解析する.
生成規則がleft-recursiveな場合は, bottom-up解析が適している.
Expression grammar (4.1) belongs to the class of LR grammars that are suitable for bottom-up parsing. ... However, it cannot be used for
top-down parsing because it is left recursive [4]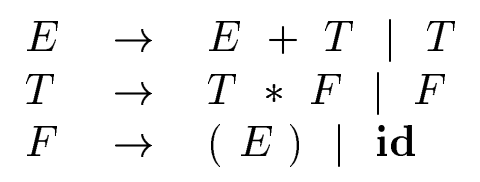
一方で, 生成規則がnon-left-recursiveな場合は, top-down解析を行う.
The following non-left-recursive variant of expression grammar (4.1) will be used for top-down parsing: [4]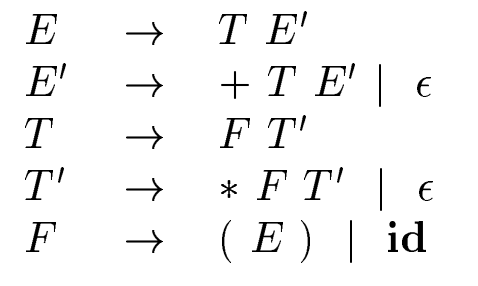
Top-Down解析
backtrackingが必要かどうかで解析方法が異なる.
Recursive-Descent Parsing with back-tracking
ある変数Aの生成規則が複数ある時に, それら全てを試す. 一つ目の生成規則が失敗したら二つ目の生成規則を適用, .二つ目の生成規則が失敗したら三つ目の生成規則を適用…のように繰り返す. 全ての規則で失敗した時にエラーを返す.
ただし, この方法は非効率だし, 無限ループの可能性があるためあまり使われない [4]
Even for situations like natural language parsing, backtracking is not very efficient, and tabular methods such as the dynamic programming algorithm of Exercise 4.4.9 or the method of Earley (see the bibliographic notes) are preferredA left-recursive grammar can cause a recursive-descent parser, even one with backtracking, to go into an in
finite loop. That is, when we try to expand a nonterminal A, we may eventually
find ourselves again trying to expand A without having consumed any input.Predictive Parsing
ある固定の数を先読みすることで, 適用するべき生成規則を確定する方法.
まずは, どの生成規則を適用するかの判定に使う二つの関数(First と Follow)を用意する. これはbottom-upでも使用可能.
First and Follow [4]
αは, 任意の文法の記号(終端記号または非終端記号)からなる文字列
First(α)
αから得られる文字列の最初の文字を表す終端記号の集合
Aは非終端記号
Follow(A)
どこかのタイミングでAの直後に存在する終端記号.
the set of terminals "a" such that there exists a derivation of the form S ⇨* αAaβ, for some α and βFirstとFollowの構成方法は[4]を参照.
LL(1)文法
以下の要素を満たす時, その言語はLL(1)文法と定義され, 1文字先読みを行うトップダウンの解析器によって解析可能 [4].
任意の相異なる二つの生成規則 A -> α | β について以下の条件を満たす.
- αとβの両方が, aから始まる文字列になることはない
2. αとβの両方が, 空文字になることはない(たかだか一個だけ空文字になる)
3. もしβ =>* ε なら, αから得られるどの文字列の最初の終端記号も, Aの直後に来る終端記号になることはない. α =>* ε の場合はその逆.
Predictive Parsing Table
先ほど定義した, FirstとFollowの情報から M[A, a]を構成. Aは非終端記号で, aは終端記号.
各生成規則 A -> α について以下を行う
- First(α)に含まれる各終端記号
aに関して, M[A, a]に A -> α を追加. - もしεがFirst(α)に含まれている場合, Follow(A)に含まれる各終端記号
b(または$)に関して, M[A, b(または$)]に A -> α を追加する.
Nonrecursive Predictive Parsing

構文解析器の実装
20. Valid Parenthesesをもとに, 括弧の組を構文解析する.
括弧を表す文脈自由文法は,
V = {S, C}
T = { "(", ")", "{", "}", "[", "]" }
Pは以下で表される生成規則の集合
S -> SS | (S) | {S} | [S] | ε
non-left-recursiveに書き換えると以下のようにも表せる.
S -> CS | ε
C -> (S) | {S} | [S]
G = {V, T, P, S}
L(G) = {w | wは有効な括弧からなる文字列}実装は以下の通り
class Parser:
def __init__(self, terminals, nonterminals, rules, start_symbol):
self.terminals = terminals
self.nonterminals = nonterminals
self.rules = rules
self.start_symbol = start_symbol
self.follow_memo = {}
self.parsing_table = {}
self._construct_parsing_table()
def first(self, string):
if len(string) == 1:
if string == "#":
return set(["#"])
if string in self.terminals:
return set([string])
result = set()
for produced_string in self.rules[string]:
result = result | self.first(produced_string)
return result
result = set()
for symbol in string:
symbol_first_result = self.first(symbol)
if "#" not in symbol_first_result:
result = result | symbol_first_result
return result
symbol_first_result.remove("#")
result = result | symbol_first_result
result.add("#")
return result
def follow(self, nonterminal):
if nonterminal not in self.nonterminals:
raise ValueError(f"{nonterminal} is not non-terminal")
if nonterminal in self.follow_memo:
return self.follow_memo[nonterminal]
result = set() if nonterminal != self.start_symbol else set(["$"])
for production_head, produced_strings in self.rules.items():
for produced_string in produced_strings:
nonterminal_idx = produced_string.find(nonterminal)
if nonterminal_idx == -1:
continue
while nonterminal_idx != -1:
remaining_string = produced_string[nonterminal_idx + 1:]
if remaining_string:
remaining_string_first_res = self.first(remaining_string)
if "#" not in remaining_string_first_res:
result = result | remaining_string_first_res
else:
production_head_follow_result = self.follow(production_head) if production_head != nonterminal else set()
result = result | production_head_follow_result | (remaining_string_first_res - set(["#"]))
else:
production_head_follow_result = self.follow(production_head) if production_head != nonterminal else set()
result = result | production_head_follow_result
nonterminal_idx = produced_string.find(nonterminal, nonterminal_idx + 1)
self.follow_memo[nonterminal] = result
return result
def _construct_parsing_table(self):
for nonterminal in self.nonterminals:
self.parsing_table[nonterminal] = {}
for terminal in self.terminals + ["$"]:
self.parsing_table[nonterminal][terminal] = []
for production_head, produced_strings in self.rules.items():
for produced_string in produced_strings:
produced_string_first_result = self.first(produced_string)
if "#" in produced_string_first_result:
head_follow_result = self.follow(production_head)
for terminal in head_follow_result:
self.parsing_table[production_head][terminal].append({production_head : produced_string})
produced_string_first_result.remove("#")
for terminal in produced_string_first_result:
self.parsing_table[production_head][terminal].append({production_head : produced_string})
# print(self.parsing_table)
return
def parse(self, input):
end_idx = len(input)
input = input + "$"
stack = ["$", self.start_symbol]
processing_idx = 0
while stack[-1] != "$":
symbol = stack.pop()
input_char = input[processing_idx]
if symbol == input_char:
processing_idx += 1
continue
if symbol in self.terminals:
return False
if not self.parsing_table[symbol][input_char]:
return False
production_rules = self.parsing_table[symbol][input_char]
if len(production_rules) >= 2:
return False
production_rule = production_rules[0]
produced_string = production_rule[symbol]
if produced_string != "#":
for produced_char in produced_string[::-1]:
stack.append(produced_char)
return processing_idx == end_idx
class Solution:
def isValid(self, s: str) -> bool:
nonterminals = ["S", "C"]
terminals = ["(", ")", "{", "}", "[", "]", "e"]
rules = {
"S" : ["CS","#"],
"C" : ["(S)", "{S}","[S]"]
}
start_symbol = "S"
parser = Parser(terminals, nonterminals, rules, start_symbol)
return parser.parse(s)参考文献
[2] GeeksforGeeks. (2025). Difference between Context Free Grammar and Regular Grammar
[3] Wikipedia. (2025). Context-sensitive grammar
[4] Aho. et.al. (1986). Compilers: Principles, Techniques, and Tools Second Edition.
コメントを残す